
Двадцатый очерк из цикла «Создатели» посвящен Софье Васильевне Ковалевской — выдающемуся математику, первой женщине в истории, ставшей профессором математики. Она родилась в Москве, стала ученицей Карла Вейерштрасса в Берлине и коллегой Гёсты Миттаг-Леффлера в Стокгольмском университете. Совместно с RASA (Russian-American Science Association) T-invariant продолжает публикацию серии биографических очерков «Создатели».
«Я чувствую, что предназначена служить истине — науке, и прокладывать новый путь женщинам, потому что это значит — служить справедливости». Софья Ковалевская
Софья Васильевна Ковалевская (урожденная Корвин-Круковская) родилась 15 января 1850 года в Москве. Ее отец Василий Васильевич Корвин-Круковский принадлежал к древнему польскому дворянскому роду. Он прошел артиллеристом Кавказскую кампанию, сделал отличную военную карьеру и вышел в отставку в звании генерал-лейтенанта (третий класс в табели о рангах). Когда родилась Софья, семья жила в Москве, где отец был начальником Московского арсенала. В 1858 году Василий Васильевич переехал с семьей в принадлежавшую ему усадьбу Полибино (Витебская губерния, ныне — Псковская область).
Мать Софьи Васильевны — Елизавета Федоровна (урожденная Шуберт) была дочерью Федора Федоровича Шуберта, генерала от инфантерии (второй класс в табеле о рангах) — геодезиста и топографа. Дед Елизаветы Федоровны (и прадед Софьи) — Федор Иванович Шуберт (Friedrich Theodor von Schubert) — был астрономом, но больше он занимался практическими вопросами. Он возглавлял Астрономическую обсерваторию Петербургской академии наук, располагавшуюся в верхних этажах Кунсткамеры, по его инициативе были созданы морские астрономические обсерватории в Николаеве и Кронштадте. Он писал научно-популярные книги по астрономии и руководства для наблюдателей. Один из его курсов был переведен на французский по предложению Пьера-Симона Лапласа. Спустя 70 лет после выхода этого курса правнучка Федора Ивановича опубликует работу, где она серьезно поправит решение Лапласа, которое он дал задаче о кольцах Сатурна.
У Сони была сестра — Анна, старше ее на 6 лет, и брат Федор — на пять лет младше.
Полибино

Впервые о математике Софья Ковалевская услышала в раннем детстве и не на уроке. В своих «Воспоминаниях о детстве», написанных в конце 1880-х, она рассказывает о своем дяде Петре Васильевиче — старшем брате ее отца. Жизнь его сложилась трудно, даже трагически. «Вследствие… слабости характера он был признан в детстве неспособным к военной службе, единственной считавшейся в то время приличной для столбового дворянина», — пишет Ковалевская, кем признан, она не уточняет. Потом он женился на женщине, которую беззаветно любил всю жизнь, но супруга его оказалась крайне несдержанным и жестоким человеком. Она бросала его рукописи и книги в печь, била его туфелькой по щекам. А он боялся только, чтобы она не ушиблась. Ее убили собственные крестьяне — задушили подушками. Петр Васильевич очень тяжело переживал эту потерю. Он приезжал к брату и подолгу жил у него. У отца Ковалевской была большая библиотека, он выписывал журналы, и его брат погружался в единственное занятие, которое давало ему отдохновение, — он читал, а потом пересказывал домашним прочитанное и обсуждал удивлявшие его научные открытия. Говорил он и о математике.
Ковалевская пишет: «Хотя он математике никогда не обучался, но питал к этой науке глубочайшее уважение. Из разных книг набрался он кое-каких математических сведений и любил пофилософствовать по их поводу, причем ему часто случалось размышлять вслух в моем присутствии. От него услышала я, например, в первый раз о квадратуре круга, об асимптотах, к которым кривая постоянно приближается, никогда их не достигая, о многих других вещах подобного же рода,— смысла которых я, разумеется, понять еще не могла, но которые действовали на мою фантазию, внушая мне благоговение к математике как к науке высшей и таинственной, открывающей перед посвященными в нее новый чудесный мир, недоступный простым смертным».

О какого рода асимптотах говорил дядя, мы, конечно, не знаем, их слишком много разных. Но вот то, что касается «квадратуры круга», гораздо определеннее. Это задача на построение, которую сформулировали еще греки. Они же и ввели главное правило: все построения надо выполнить с помощью только циркуля (с любым раствором) и линейки (бесконечной и без делений). Эти идеальные приборы были своего рода платоновскими идеями кругового и прямолинейного движения, и использовать следовало именно их. По-видимому, это ограничение и было «канонизировано» Платоном. Такими очень скромными средствами греки решили множество задач. Их остроумие и находчивость — замечательны. Но вот «квадратура круга» им никак не давалась: построить квадрат, по площади равный кругу, они не смогли. Задача оставалась нерешенной до XIX века.
В 1852 году в Ганновере родился Карл Линдеман. В то время, когда Соня была девочкой и слушала рассказы дяди, Карл вряд ли всерьез помышлял о «квадратуре круга» и совершенно точно не представлял, какую роль ему предстоит сыграть в истории этой задачи. Он вырос, стал математиком, преподавал, защищал диссертации. Жизнь складывалась, работа увлекала.
В 1882 году, когда Ковалевская, будучи уже признанным математиком, собиралась читать лекции в Стокгольмском университете, Линдеманн решил «квадратуру круга». Решение задачи, которой как минимум две с половиной тысячи лет, — это серьезный результат. Линдеман доказал, что число π — трансцендентное, а значит отрезок длиной π с помощью циркуля и линейки построить нельзя (уже было известно, что так можно построить только алгебраические числа). А значит «квадратура круга» — неразрешима. Результат Линдемана опубликовали сразу в двух изданиях: в Берлине его напечатал Карл Вейерштрасс, а в Париже — Шарль Эрмит. И тот и другой были хорошо знакомы с Ковалевской, Эрмита можно назвать ее другом, а Вейерштрасс — ее учитель. И она просто не могла не узнать о таком крупном достижении как доказательство Линдемана. И в своих «Воспоминаниях» она упомянула, что о квадратуре круга впервые услышала от дяди. Но это было сильно позднее.
Были ли Ковалевская и Линдеман знакомы лично, установить не удалось, но они вполне могли бы встретиться, например, на Первом международном конгрессе математиков в Цюрихе в 1897 году. Если бы Ковалевская дожила (а ей было бы 47 лет), по уровню результатов и степени включенности в математическую жизнь она была достойна сделать доклад на конгрессе. Но и на этом, и на многих следующих конгрессах выступали только мужчины. Впервые женщина сделала доклад на Конгрессе в 1932 году, — это была Эмми Нётер.

Семья Корвин-Круковских жила в Полибино (Витебская губерния, Невельский уезд, ныне Псковская область, Великолукский район) — живописной усадьбе на краю заповедного огромного бора, в котором полно было всякой живности и водились медведи. Соня училась музыке, арифметике, языкам. Она упоминает о своих гувернантках — сначала француженке, потом — англичанке. Но Ковалевская ничего не говорит о своих уроках немецкого. Допустить, что она не знала немецкий — невозможно, например, потому, что немецкий — это родной язык ее матери. Но трудно представить, что Елизавета Федоровна занималась с дочерями немецким — Ковалевская буквально по крупицам собирает моменты, когда ей удавалось пообщаться с мамой, и если бы еще были уроки немецкого, она бы непременно их упомянула. Неужели немецкий Соня усвоила прямо из воздуха? Ответ на этот вопрос есть и довольно неожиданный. Мы расскажем об этом подробно во второй части, а пока только отметим, что немецким Ковалевская начала заниматься поздно, — когда ей уже исполнилось 16 лет.

Так получилось, что вообще все образование Ковалевской — от азбуки до докторской диссертации — было домашним. Она, может быть, и хотела бы учиться «как все», то есть как мужчины, но такой возможности мужчины, управлявшие государствами, академиями и университетами, ей не дали.
В автобиографическом очерке, написанном в 1890 году, Ковалевская рассказывает о первых этапах своего математического образования. Первым, кто знакомил ее с математикой, был домашний учитель Иосиф Игнатьевич Малевич. Это была арифметика и основы алгебры и геометрии. Поначалу математика будущему математику совсем не понравилась. Она показалась Соне какой-то сухой. Но, чтобы не огорчать отца, Соня старалась, старалась и неожиданно вошла во вкус. Ей как-то очень быстро все становилось ясно. Девочка сразу видела глубоко. Все будущие ее учителя от Страннолюбского до Вейерштрасса отмечали необыкновенную скорость, с которой девочка, потом девушка, потом профессиональный математик проникала в суть задачи, видела весь лабиринт решений и различала тот путь, который ведет к разгадке. И часто этот путь оказывался проще и прямее, чем те решения, которые находили другие математики. Как будто ее мозг был специально так устроен, чтобы математические знания ложились в него оптимально и выстраивались в изящную картину.
Стена Остроградского
В «Воспоминаниях о детстве» Ковалевская рассказывает случайный, вроде бы, эпизод, который сильно повлиял на ее математическое образование и мышление.
«Говоря об этих первых моих соприкосновениях с областью математики, я не могу не упомянуть об одном очень курьезном обстоятельстве, тоже возбудившем во мне интерес к этой науке. Когда мы переезжали на житье в деревню, весь дом пришлось отделать заново и все комнаты оклеить новыми обоями. Но так как комнат было много, то на одну из наших детских комнат обоев не хватило, а выписывать-то обои приходилось из Петербурга, это было целой историей, и для одной комнаты выписывать решительно не стоило. Все ждали случая, и в ожидании его эта обиженная комната так и простояла много лет с одной стеной, оклеенной простой бумагой. Но, по счастливой случайности, на эту предварительную оклейку пошли именно листы литографированных лекций Остроградского о дифференциальном и интегральном исчислении, приобретенные моим отцом в его молодости.
Листы эти, испещренные странными, непонятными формулами, скоро обратили на себя мое внимание. Я помню, как я в детстве проводила целые часы перед этой таинственной стеной, пытаясь разобрать хоть отдельные фразы и найти тот порядок, в котором листы должны бы следовать друг за другом. От долгого ежедневного созерцания внешний вид многих формул так и врезался в моей памяти, да и самый текст оставил по себе глубокий след в мозгу, хотя в самый момент прочтения он и остался для меня непонятным.
Когда, много лет спустя, уже пятнадцатилетней девочкой, я брала первый урок дифференциального исчисления у известного преподавателя математики в Петербурге, Александра Николаевича Страннолюбского, он удивился, как скоро я охватила и усвоила себе понятия о пределе и о производной, «точно я наперед их знала». Я помню, он именно так и выразился. И дело, действительно, было в том, что в ту минуту, когда он объяснял мне эти понятия, мне вдруг живо припомнилось, что все это стояло на памятных мне листах Остроградского, и самое понятие о пределе показалось мне давно знакомым».

Норберт Винер в своей книге «Я — вундеркинд» вспоминает, как будучи ребенком, читал очень сложные книги, например, Платона. Винер спрашивает себя: понимал ли я хотя бы что-то? И шире: есть ли вообще хоть какая-то польза от такого чтения? И отвечает: да, есть. Если ребенок и не понимает того, что читает, он при сосредоточенном внимании может запомнить, о чем идет речь, как запоминают мелодию или картину. И потом, будучи уже взрослым, человек может вспомнить прочитанное и понять. Тогда приобретенные в детстве знания перейдут из латентного состояния в явное и станут настоящим фундаментом, на котором строится картина мира. И это — надежный фундамент.

Математические формулы — это ведь не текст, это иероглифы или картины, над которыми нужно долго и сосредоточенно размышлять, беглого чтения здесь недостаточно. Но понять можно многое. Что-то подобное и произошло с Ковалевской.
Соседом Корвин-Круковских по имению был профессор Морской академии Николай Тыртов. Он часто бывал у них. И он подарил (не Соне, конечно, а ее отцу) написанный им учебник физики. Напомним, откуда на стене появились литографические копии лекций Остроградского: Василий Васильевич был артиллеристом, и как раз Остроградский учил его математике. Так что разобраться с учебником Тыртова он мог бы легко, если бы, конечно, захотел. Но увлеченным читателем этой книги стал не он.
Ковалевская пишет в автобиографическом очерке: «Я попробовала читать эту книгу, но, к своему огорчению, в отделе об оптике встретила тригонометрические формулы, синусы, косинусы, тангенсы. Что такое синус? Перед этим вопросом я становилась в тупик и для разрешения загадки попробовала обратиться к Малевичу. Но так как это не входило в его программу, то он ответил мне, что не знает, что такое синус. Тогда, сообразуясь с формулами, бывшими в книге, я попыталась объяснить сама. При этом, по странному совпадению, я пошла тем же путем, который употреблялся исторически, т. е. вместо синуса брала хорду. Для малых углов эти величины почти совпадут друг с другом. А так как у Тыртова во все формулы входили только бесконечно малые углы, то, при взятом мною основном определении, эти формулы отлично сходились. На этом я и успокоилась.
Затем, через несколько времени, когда у меня зашла речь с Тыртовым по поводу его книги, то он сперва усомнился в том, чтоб я могла ее понимать, и на мое заявление, что я прочла ее с большим интересом, сказал: «Ну, вот и хвастаетесь». Но когда я рассказала ему, каким путем я дошла до объяснения тригонометрических формул, то он совсем переменил тон. Он сейчас же отправился к моему отцу и горячо стал убеждать его в необходимости учить меня самым серьезным образом. При этом он сравнил меня с Паскалем. Тогда, после некоторого колебания, отец мой согласился взять мне в учителя А. Н. Страннолюбского, с которым мы вслед за тем принялись успешно за работу и в течение зимы прошли аналитическую геометрию, дифференциальное и интегральное исчисления».
(Это много и это очень быстро — примерно объем первых двух курсов современного мехмата.)
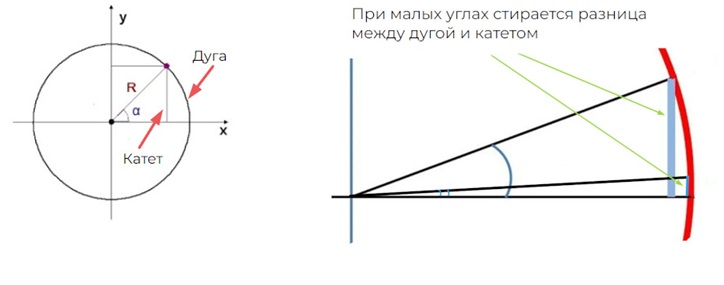
Это открытие и сделала самостоятельно юная Соня.
Занятия со Страннолюбским проходили уже не в Полибино, а в Санкт-Петербурге, куда 15-летнюю Соню отпустил Василий Васильевич на зиму вместе с матерью.
Тыртов упомянул великого французского математика, скорее всего, неслучайно. Не только, чтобы польстить Василию Васильевичу (кому не будет приятно услышать, что его дочь — гений), но и чтобы немного его попрекнуть. Корвин-Круковский был человек образованный и наверняка знал историю юного Блеза Паскаля.
Этьен Паскаль — отец Блеза — был человеком не чуждым науке. Он рано овдовел и воспитывал и обучал сына сам. Но у него была строгая схема. Чтобы не перегружать ребенка, он решил, что сначала следует обучать его языкам, а уже потом математике. И заниматься геометрией он мальчику запретил. Но что-то Блез слышал от отца и начал играть в геометрию, которая его очень увлекала. Монетки стали кругами, столы — прямоугольниками, треуголки (шляпы) — треугольниками. Эти игры его далеко завели. Мальчик в совсем юном возрасте самостоятельно доказал 32-ю теорему Евклида — о сумме углов треугольника. Он показал, что три угла треуголки в сумме равны двум углам стола. Когда отец это увидел, он прекратил чинить какие-либо препятствия сыну и просто открыл ему свою научную библиотеку. Отец Ковалевской упорствовал не намного дольше.
Здесь стоит отметить важный момент, который потом стал характерной чертой математика Софьи Ковалевской. Она старалась увидеть то, над чем она думает. И самые сильные ее результаты (в первую очередь, работа о вращении асиметричного волчка) связаны, пусть и со сложными, но «видимыми» объектами. А в математике «увидеть» — не всегда просто, особенно в тех абстрактных областях, которыми Ковалевской предстояло заниматься профессионально. Академик Владимир Арнольд неоднократно писал: чтобы понять — необходимо увидеть, увидеть геометрию изучаемого объекта. Если ты не видишь — ты еще ничего не понял. Соня догадалась заменить непонятную ей функцию (абстракцию) на ясно видимую хорду и сделала эту замену правильно. Этот случай как простая модель показывает, как будет работать ее талант.
Тыртов вряд ли догадывался, что его сравнение Сони с Паскалем имеет и еще одну грань: Блез Паскаль прославился не только (да, может быть, и не столько) математикой. Семен Гиндикин приводит в своем очерке о Паскале слова Льва Толстого, который читал «чудного Паскаля», «человека великого ума и великого сердца» и «не мог не умилиться до слез, читая его и сознавая свое полное единение с этим умершим сотни лет тому назад человеком». Конечно, Толстой читал «Мысли» Паскаля, а не его трактат о конических сечениях.
«Ворованный воздух»
Примерно в возрасте 12 лет у Ковалевской проснулось и другое увлечение, даже, пожалуй, настоящая страсть — поэзия. Ее англичанка сделала буквально все, чтобы эта страсть охватила девочку и больше никогда не отпускала. Мисс Смит строго-настрого запретила Соне читать хотя бы что-то сверх очень скромного минимума. Она была убеждена, что настоящей леди много читать не следует. Даже детские книги мисс Смит сначала читала сама, и только потом разрешала их читать Соне. А читала англичанка медленно, и девочка постоянно испытывала настоящий книжный голод. И перед глазами был дядя — Петр Васильевич, который книги просто глотал. Вообще-то трудно представить лучшее состояние для погружения в чтение и литературу. Книги для Сони были буквально — «ворованный воздух». Она тайком пробиралась в библиотеку, брала первую попавшуюся книгу и читала. Ей было не важно, первый это том длинного французского романа или второй. Сразу читать второй было даже интереснее — Соня реконструировала события, которых не знала. Она читала и чутко прислушивалась: не идет ли по лестнице мисс Смит? Обычно ей удавалось вовремя услышать шаги англичанки, девочка успевала выскочить из библиотеки и сделать вид, что она играет в мяч в соседней комнате. Но иногда книга настолько захватывала, что Соню возвращал к реальности грозный окрик гувернантки. Дальше — настоящий ужас. Англичанка приказывала Соне идти к отцу и рассказывать о своих прегрешениях. Это было испытание. Какое-то время Соня была послушнейшим ребенком, но потом страсть к книгам все равно побеждала. (Ковалевская пишет, что и математические книги мисс Смит тоже не одобряла, и «Курс алгебры» Бурдона девочка читала тайком под одеялом)

При таких условиях чтение становится запретным плодом. Но как же он сладок! Соня влюбилась в русскую поэзию — баллады Жуковского, лермонтовский «Мцыри», пушкинский «Кавказский пленник». И начала сочинять стихи. Она вспоминает: «Однако гонение это на мои стихи не помогало. В двенадцать лет я была глубоко убеждена, что буду поэтессой. Из страха гувернантки я не решалась писать своих стихов, но сочиняла их в уме, как старинные барды, и поверяла их моему мячику. Погоняя его перед собой, я несусь, бывало, по зале и громко декламирую два моих поэтических произведения, которыми особенно горжусь: «Обращение бедуина к его коню» и «Ощущения пловца, ныряющего за жемчугом». В голове у меня задумана длинная поэма «Струйка», нечто среднее между «Ундиной» и «Мцыри», но из нее готовы пока только первые десять строф. А их предполагается 120».
Да, все эти сочинения необходимо было хранить в памяти, потому что если англичанка их найдет, она может прочитать их за ужином, да еще так исковеркает, что все будут смеяться. А потом она эти бесценные строки порвет и выбросит. (Буквально сцена из клипа «Another Brick in the Wall»).
Ковалевская писала стихи всю жизнь. Она писала художественные произведения по-русски и по-шведски. Ее печатали ведущие литературные журналы России, в том числе «Вестник Европы», где в 7 и 8 номерах за 1890 год вышли ее «Воспоминания о детстве». Эти «Воспоминания» принесли ей признание уже как писателю, а не только как математику.
Осенью 1890 года Ковалевская писала своей корреспондентке: «Я понимаю, что вас так удивляет, что я могу заниматься зараз и литературой и математикой. Многие, которым никогда не представлялось случая более узнать математику, смешивают ее с арифметикой и считают ее наукой сухой и aride (франц. сухой, бесплодный — ВГ). В сущности же это наука, требующая наиболее фантазии, и один из первых математиков нашего столетия говорит совершенно верно, что нельзя быть математиком, не будучи в то же время и поэтом в душе. Только, разумеется, чтобы понять верность этого определения, надо отказаться от старого предрассудка, что поэт должен что-то сочинять несуществующее, что фантазия и вымысел — это одно и то же. Мне кажется, что поэт должен видеть то, чего не видят другие, видеть глубже других. И это же должен и математик. Что до меня касается, то я всю мою жизнь не могла решить: к чему у меня больше склонности — к математике или к литературе? Только что устанет голова над чисто абстрактными спекуляциями, тотчас начинает тянуть к наблюдениям над жизнью, к рассказам, и, наоборот, в другой раз вдруг все в жизни начинает казаться ничтожным и неинтересным, и только одни вечные, непреложные научные законы привлекают к себе. Очень может быть, что в каждой из этих областей я сделала бы больше, если бы предалась ей исключительно, но тем не менее я ни от одной из них не могу отказаться совершенно».
Когда Ковалевская ссылается на «одного из первых математиков нашего столетия», она цитирует в пересказе письмо к ней Карла Вейерштрасса. Обнародовал это письмо Гёста Миттаг-Леффлер на Втором международном конгрессе математиков в Париже в 1900 году, когда Ковалевской уже не было. (См. Примечание)
Мы здесь не случайно приводим такие большие цитаты из «Воспоминаний о детстве». Это — та «просторная» русская проза, о которой писал Давид Самойлов: «Учусь писать у русской прозы, Влюблен в ее просторный слог». Наверно, как Ковалевская, могли бы писать «тургеневские девушки», например, героиня «Накануне» Елена Стахова. Она напоминает Ковалевскую и смелостью, и готовностью бороться за свои идеалы. Ковалевская такую готовность продемонстрировала в полной мере.
Две сестры и брат
Две сестры — это Соня и Анюта Корвин-Круковские, а брат, нет, это не Федя, это совсем другой человек.
Анюта (Анна) была любимицей отца и матери. Она была первым ребенком в семье. Ей досталось куда больше внимания родителей, чем Соне. В отличие от Сони Анюта была яркой, ироничной, она любила быть в центре внимания. Еще будучи совсем девочкой, она проводила много времени со взрослыми, смешила и восхищала гостей своими остроумными репликами. А вот когда к гостям звали Соню, она смущалась, молчала и пряталась в нянин передник. Всем становилось неловко, и ее с облегчением отпускали обратно в детскую. Но Соня не ревновала к сестре. Она едва ли перед ней не преклонялась.
Анюта первой уехала из Полибино в Петербург. Отец был против, но ничего не мог поделать.
Почему так получилось, что в таком тихом месте как Полибино, в такой патриархальной семье выросли настолько свободные и независимые девушки? Трудно ответить на этот вопрос. Одно только можно заметить: Россия пришла в движение после освобождения крестьян в 1861 году, и это движение, часто неустойчивое и даже хаотичное, не могло не отразиться на этих талантливых и образованных девушках.
Анюта в Петербурге познакомилась с Федором Достоевским (позднее Соня тоже с ним познакомилась, и писатель был принят в петербургском доме Корвин-Круковских). Анюта напечатала в журнале братьев Достоевских «Эпоха» два своих рассказа. Ее литературный талант казался несомненным, и Соня признавала первенство литературных дарований сестры — радостно и безоговорочно. История отношений Анюты с великим писателем увела бы нас далеко в сторону, но отметим, что отношения эти едва не привели к браку. Не привели потому, что у Анюты были совсем другие планы. И есть предположение, что она стала прототипом Аглаи Епанчиной — одной из двух главных героинь «Идиота».
Анюта знала, чего она хочет: уехать из провинциальной России в просвещенную Европу, чтобы получить там университетское образование. В России получить такое образование женщина не могла. (Отметим сразу, что и в Европе это было ох как непросто, но варианты все-таки были). Чтобы уехать за границу, любая девушка должна была получить разрешение отца. Василий Васильевич дать такое разрешение был не готов. Но был и другой вариант — выйти замуж. Но нет, не для того, конечно, чтобы строить семью, а чтобы получить свободу. Анюта и ее подруга Жанна Евреинова искали себе кандидатов для фиктивного брака. Они называли таких кандидатов ласково — «консервы». И кое-кого они подобрали.

Одним из кандидатов девушки выбрали Владимира Онуфриевича Ковалевского. Он был старше Анюты на два года, закончил Императорское училище правоведения (по статусу приравненное к Царскосельскому лицею), где готовили кадры для Сената и Министерства юстиции. Перед Ковалевским открывалась надежная карьерная лестница — вплоть до самых верхних ступеней табели о рангах. Но, может быть, эта предопределенность его и отпугнула. Он, только начав служить в департаменте герольдии Сената, попросил отпуск по болезни и уехал в Европу. Там он познакомился с Герценом и Дарвином и увлекся палеонтологией: Ковалевский хотел подтвердить дарвиновскую теорию происхождения видов ископаемыми находками. Дарвин сочувствовал его работе, и они находились в переписке. Возвращаться на государственную службу Ковалевский совершенно не собирался. Он был человек независимых взглядов, сочувствовал борьбе женщин за равноправие и готов был помогать их просвещению. В дополнение к этим его положительным качествам Шустянка — небольшое, совсем не генеральское поместье его отца — было недалеко от Полибино. В общем, готовый «консерв».

Вообще-то Ковалевского Анюта готовила для себя, но когда он увидел младшую сестру, неожиданно проявил характер и заявил, что на фиктивный брак он согласен, но только не со старшей сестрой, а с младшей. Анюта как будто не очень расстроилась и уступила выгодную партию сестре. (Ей не пришлось заключать фиктивный брак, отец отпустил ее Европу и даже назначил содержание, и там она влюбилась и вышла замуж по-настоящему.)
Странный это был «фиктивный брак». Ковалевский пишет брату: «Несмотря на свои 18 лет, воробышек (Соня — ВГ) образована великолепно, знает все языки, как свой собственный, и занимается до сих пор главным образом математикой, причем проходит уже сферическую тригонометрию и интегралы — работает, как мужчина, с утра до ночи и при всем этом жива, мила и очень хороша собой. Вообще это такое счастье свалилось на меня, что трудно себе и представить».
Отцу жених совершенно не понравился. Какой-то он ненадежный — не служит, занимается не пойми чем (книжки какие-то издает, какое же это дело?), да и не богат. Но тут уже Соня проявила характер и сбежала из дома к жениху на целый день. И отцу пришлось смириться, иначе неизбежно поползли бы слухи, и честное имя Сони пострадало бы. Допустить такое Василий Васильевич, конечно, не мог.
Ковалевский пишет брату: «Я со всею своею опытностью в жизни, с начитанностью и напористостью не могу и вполовину так быстро схватывать и разбирать разные политические и экономические вопросы, как она; и будь уверен, что это не увлечение, а холодный разбор. Я думаю, что эта встреча сделает из меня порядочного человека, что я брошу издательство и стану заниматься, хоть не могу скрывать от себя, что эта натура в тысячу раз лучше, умнее и талантливее меня. О прилежании я уже и не говорю, как говорят, сидит в деревне по 12 часов, не разгибая спины, и, насколько я видел здесь, способна работать так, как я и понятия не имею. Вообще это маленький феномен, и за что он мне попался, я не могу сообразить».
Венчание состоялось в Полибино 27 сентября 1868 года. Вот как его описывает присутствовавшая на этом торжестве одна из Сониных теток: «Наконец появилась Соня, свежая, хорошенькая и сияющая от счастья, какой только может быть невеста». В простом платье «она, однако, выглядела очаровательно… она была так мила, что все присутствовавшие заявили, что никогда еще не видели такой прелестной невесты. Сияющее выражение лица не покидало ее ни на одну минуту во время всей церемонии; но это не было выражением поверхностного волнения, а было глубоким сознанием истинного счастья».
И вот это называется «фиктивный брак»? Когда брак перестал быть фиктивным, мы не знаем, но спустя 10 лет в семье Ковалевских родилась дочь — Софья.
А в письмах друг другу Соня и Анюта долгое время называли Ковалевского «брат».

После свадьбы Ковалевские отправились в Петербург, где Соня надеялась продолжить свое образование. Юность кончилась. Но это было только начало. Каким стало продолжение, мы рассказываем во втором очерке о Софье Ковалевской.
Примечание: Karl Weierstrass: «es ist wahr, ein Mathematiker, der nicht etwas Poet ist, wird nimmer ein vollkommener Mathematiker sein». Письмо Карла Вейерштрасса Софье Ковалевской от 27 августа 1883 года. Впервые было показано Гёстой Миттаг-Леффлером на 2-м Международном конгрессе математиков в Париже https://en.wikiquote.org/wiki/Karl_Weierstrass.